威尔逊得分计算方法
先来一个场景:假设平台售卖两款手机A和B。A手机有800人喜欢,200人不喜欢;B手机有9人喜欢,2人不喜欢。那么,用户更喜欢哪款手机?
相信这个场景,各位朋友在日常生活中、在工作中都遇到过。你们平时是如何做判断呢?希望通过今天的文章,能给大家一个新的视角、也更加科学的方案。
01
常见的衡量方法
我想,大家的第一反应应该是按照比率进行衡量吧?因此,A手机喜好率=800÷(800+200)=80%B手机喜好率=9÷(9+2)=82%
80%<82%,因此用户更喜欢B手机。
这样对吗?
看起来没毛病。毕竟喜欢率越高,代表用户更喜欢嘛!但是,相信朋友也看出了这个例子的端倪:B手机的总共的样本量才11个,虽然喜欢率高,但是样本量这么低,随便一个数据变化都会对结果产生巨大的影响。
因此,按照这种比率的方法,算出的喜欢率,“靠谱”吗?用统计学的语言,置信吗?
02
威尔逊得分
上面我们觉得按照简单的喜欢率来计算,有点难衡量。但是,如果不按照喜欢率来比较,还能如何计算呢?这就是我们今天的主题了:威尔逊得分。
(1)公式定义
先看看具体的威尔逊得分计算公式:
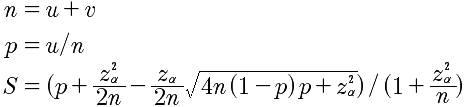
u表示正例数(喜欢),v表示负例数(不喜欢),n表示实例总数(总样本数),p表示喜欢率,z是正态分布的分位数(参数),S表示最终的威尔逊得分。得分越高,代表越喜欢的程度、喜欢的概率越大。
通常,当置信度95%的情况下,z取1.96(近似2)即可。其他常见置信水平与z取值的对应关系如下:
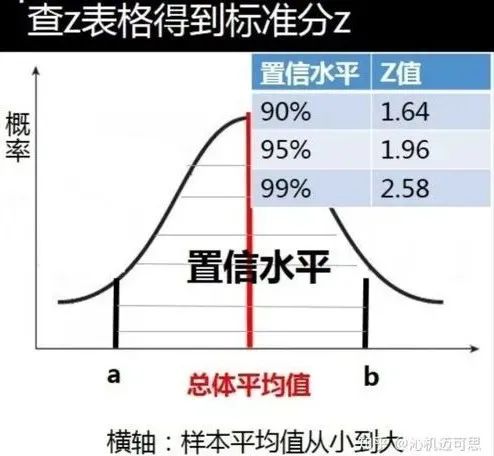
关于置信区间的概念,可以参考文章《区间估计的置信区间概念及方法》。
(2)案例验证
下面,我们根据上面的公式,计算一下我们开头案例的A手机和B手机的威尔逊得分情况。
对于A手机,n=1000,p=0.8,按照95%的置信度,取z≈2,代入威尔逊得分公式中,求得S(A)=0.77
对于B手机,n=11,p=0.82,按照95%的置信度,取z≈2,代入威尔逊得分公式中,求得S(B)=0.52
因此,0.77>0.52,A手机的威尔逊得分高于B手机,按照该算法,我们有结论:在置信度95%的情况下,虽然A手机的喜欢率不如B手机,但是有理由相信用户对A手机其实是更加喜欢的。
